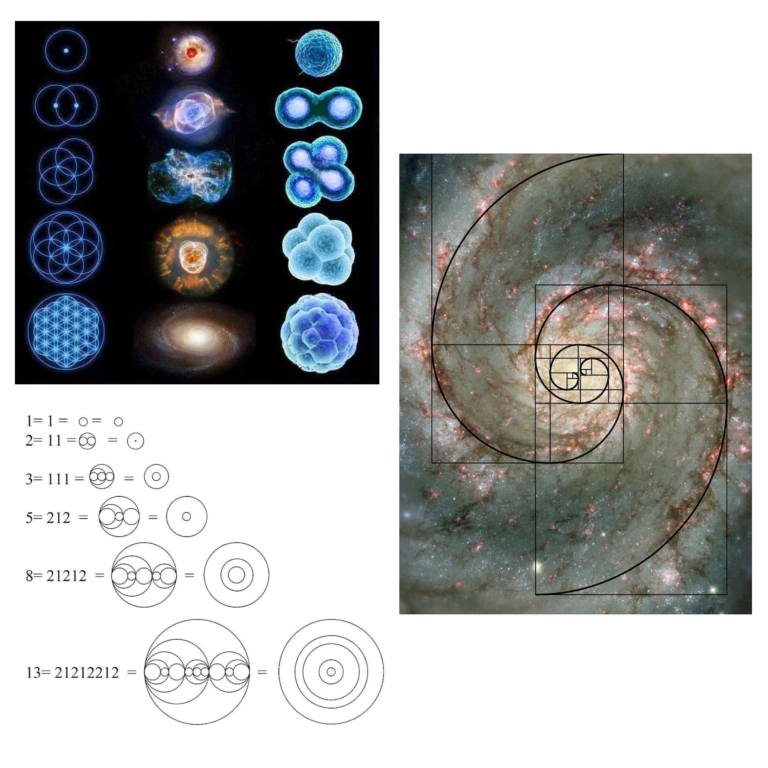
Et si Dieu était un mathématicien?
Nombre d’or, Section dorée, Divine proportion et autres appellations mystiques, sont des dénominations qui désignent un rapport arithmétique : le nombre d’or. Ce dernier n’est ni une mesure, ni une dimension, c’est un rapport entre deux grandeurs homogènes.
Des milliers de pages ont été écrites sur ce fameux nombre d’or, baptisé Φ. Il serait connu depuis la nuit des temps. On le retrouve au cœur de la grande Pyramide, dans les cathédrales gothiques, sur les façades des temples grecs et même dans la nature. Il aurait été transmis par les érudits égyptiens aux oreilles des initiés grecques, comme un secret universel et immuable.
Ainsi, dans les arts par exemple, les proportions du nombre d’or étant considérées comme gracieuses , on trouve de nombreux tableaux, monument, et sculptures qui l’exploitent. En effet, de nombreux tableaux seraient conçus selon les règles de la “divine proportion” (expression datant de 1509 avec Léonard de Vinci).
Parmi les artistes de la Renaissance, Dürer est un de ceux qui connaissait les mathématiques. Il fit évoluer les proportions de “ses nus d’Adam et Eve”, entre 1504 et 1507 après avoir été initié à la “secretissima scienta” par un maître dont il ne voulut pas révéler le nom mais qui fut sans doute le frère franciscain Luca Pacioli qui publia en 1494 la grande encyclopédie du XVe siècle.
La présence du nombre d’or dans la nature, aussi bien chez les végétaux chez les animaux et chez l’homme , suscite bien des questions dans la communauté scientifique. En effet, ce nombre d’or nous emporte toujours plus loin, au-delà de toutes limites…
Le nombre d’or
La suite de Fibonacci doit son nom au mathématicien italien Leonardo Fibonacci qui a vécut au XIIème et XIIIème siècle. Il est connu pour avoir introduit et popularisé en Europe et en Occident la numérotation indo-arabe qui a remplacé pour les calculs la notation romaine peu pratique aux opérations arithmétiques.
Mais il est aussi connu pour avoir mis en évidence une suite mathématique qui porte désormais son nom. Dans la suite de Fibonacci, il n’est pas nécessaire de mémoriser chacun des termes ou nombres de la suite (qui est d’ailleurs infinie).
Il suffit de se rappeler sa règle de construction: à l’exception des deux premiers, chaque terme de la suite est égal à la somme des deux termes qui le précèdent immédiatement, dit autrement il s’agit d’une suite de nombres dans laquelle tout nombre (à partir du troisième) est égal à la somme des deux précédents: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…
Il suffit de prendre deux nombres de départ. Les ajouter donne le troisième, puis le deuxième + le troisième donne le quatrième et ainsi de suite. Les termes de cette suite sont appelés nombres de Fibonacci.
La suite de Fibonacci possède de nombreuses propriétés très utilisées en mathématiques. Une d’entre elles est que le rapport de deux nombres consécutifs de la suite est alternativement supérieur et inférieur au nombre d’or, un nombre remarquable qui vaut exactement 1.61803398…
Définition
En effet: 13/8 = 1.625 ; 21/13 = 1.61538… ; 34/21 = 1.61904 et ainsi de suite… plus on avance dans la suite de Fibonacci, plus l’écart s’amenuise, et plus le rapport des deux nombres successifs (le plus grand / le plus petit) tend vers la valeur du nombre d’or 1,61803…
En géométrie, le nombre d’or est la valeur qui correspond au rapport entre deux longueurs a (la plus grande) et b (la plus petite) telles que (a+b)/a = a/b.
Constructions géométriques et architectures
Par exemple, le Parthénon d’Athènes, fait apparaître le nombre d’or à plusieurs reprises .


Le Parthénon s’inscrit dans un rectangle doré, c’est-à-dire tel que le rapport de la longueur à la hauteur est égal au nombre d’or.
Sur la figure : DC/DE =Φ
Sur la toiture du temple, GF/GI = Φ
Le rectangle d’or
Un rectangle d’or est un rectangle dont le rapport longueur sur largeur est égal au nombre.
On part d’un côté de longueur 1/2 pour construire un triangle rectangle dont les côtés de l’angle droit mesurent 1 et 1/2.
En utilisant le théorème de Pythagore, l’hypoténuse mesure :
( 1 +√5) / 2 = Φ
Il suffit de terminer le rectangle d’or dont les côtés mesurent 1 et Φ .
Le rapport de leurs longueurs est égal au nombre d’or et le rectangle est dit d’or. Ce rectangle est harmonieux, son équilibre flatte l’œil et statistiquement il a la préférence lorsqu’on le compare à d’autres rectangles de formes diverses.
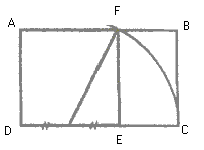
A partir de ce rectangle d’or ABCD on à tracer un nouveau rectangle d’or FBCE…

Au bout d’ un certain temps, en répétant plusieurs fois l’opération, on obtient une figure ressemblant a cela.
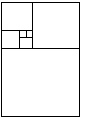
L’ on peut ainsi tracer la spirale d’or qui nous sera très utile car on la retrouve dans la nature et chez l’homme.
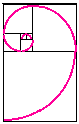
Le triangle d’or
Un triangle d’or est un triangle isocèle dont les longueurs des côtés sont dans le rapport du nombre d’or.


Pentagone régulier et nombre d’or.

Le pentagone régulier est une figure d’or car la proportion entre une diagonale et un côté est le nombre d’or.
AC/AD = Φ
Dans ce pentagone régulier le triangle ABC et le triangle ACD sont tous deux des triangles isocèles dont les longueurs des côtés sont dans le rapport du nombre d’or : ce sont deux triangles d’or.
On les retrouve aussi bien dans la faune que dans la flore.
Le nombre d’or chez les végétaux
Dans la nature, on retrouve très souvent des motifs basé sur la suite Fibonacci et sur le nombre d’or. Il semblerait que la nature marque une prédilection pour la suite de Fibonacci et pour le nombre d’or.
Fruit et légume
Ananas
On le retrouve ainsi dans l’ananas. Les écailles que l’on voit sur ce fruit forment des spirales qui comportent un nombre précis de ces même écailles.

Le chou-fleur
De même, on trouve des spirales dans le chou-fleur : en observant ce légume, on peut voir que l’on peut former une spirale en rejoignant les petits espaces formés entre deux petits morceaux.

Dans le schéma ci-dessus, on voit bien qu’on peut faire ressortir deux types de spirale :
· celles orientées dans le sens direct (rouge) : 5 spirales
· celles orientées dans le sens indirect (bleu) : 8 spirales
5…8… encore deux termes qui nous amènent vers Φ .
Botanique
On retrouve le nombre d’or, la suite de Fibonacci plus précisément, chez les fleurs. On sait déjà qu’une marguerite a un lien direct avec les termes de la suite de Fibonacci (au niveau des spirales… ).

Mais il se trouve qu’après une observation minutieuse, on se rend vite compte qu’il n’y a pas beaucoup de fleur à 4, 6, 9, 12 pétales par exemple, alors qu’une écrasante majorité des fleurs possèdent 3,5,8,13 pétales… c’est à dire un nombre de pétales qui appartient à la suite de Fibonacci.
Il semble donc bel et bien y avoir une constante lorsque l’on compte le nombre de pétales d’une fleur. Les fleurs qui possèdent un nombre de pétales qui n’appartient pas à la suite de Fibonacci sont peu nombreuses face à celle qui possèdent cette caractéristique..
C’est peut-être une des raisons pour lesquelles les trèfles à quatre feuilles sont rares (c’est peut-être parce que ces plantes ont souvent 5 ou 3 feuilles, ce qui rend les trèfle à 4 feuilles relativement rares.. d’où –en partie- l’histoire du trèfle à 4 feuilles qui porte bonheur…)
Les arbres
Les nombres de branches développées sur un arbre chaque année sont également des termes consécutifs de la suite de Fibonacci

La pomme de pin
Ces spirales sont aussi apparentes dans les pommes de pins.
Même principe : deux types spirales, l’une dans un sens et l’autre dans un sens contraire, des nombres de spirales dans chacun des différent types qui sont deux termes successifs de la suite de Fibonacci.

L’étude détaillée de ces spirales a conduit aux conclusions suivantes :
-les spirales sont logarithmiques
-le nombre des spirales dans le sens des aiguilles d’une montre et celui en sens inverse sont les termes successifs de la suite de Fibonacci.
Mais cette présence ne se limite pas aux plantes… On le retrouve aussi chez les animaux, et en particulier chez l’Homme.
Le nombre d’or chez les animaux
Les spirales sont également présentes chez les animaux : la coquille d’escargot ou le nautile, un animal marin primitif, qui existait déjà il y a des centaines de millions d’années.

L’animal reste dans la dernière chambre au tout début. En grandissant, il occupe un volume plus gros. Pour pouvoir rester dans une coquille, il va synthétiser un nouveau compartiment, basé sur le modèle de la chambre initiale, mais plus gros cette fois ci. Et il continue ainsi de suite, donnant naissance à une spirale d’or.
Divers animaux
Par exemple, chez ces trois animaux le nombre d’or est présent : en faisant le rapport de la longueur jaune par le rapport de la longueur verte, on obtient constamment le nombre d’or.

Particularité des abeilles
Les abeilles possèdent un système reproductif assez particulier : la femelle peut stocker le sperme des mâles pendant plusieurs mois et décider si elle le fécondera ou non. Un œuf fécondé donne une femelle, un œuf non fécondé donne un mâle.
En supposant qu’aucune abeille ne meure nous obtenons le schéma suivant :

On peut constater que la suite de Fibonacci est présente dans le schéma ci-dessus, le nombre d’individus est égal aux nombres de cette suite. A chaque génération le nombre de femelles et de mâles, et la somme des mâles et des femelles sont trois nombres consécutifs de la suite : pour la 6ème ligne nous avons 5 mâles et 8 femelles, la somme des deux fait 13, ces trois nombres se suivent dans la suite de Fibonacci.
La divine proportion chez l’homme
Depuis l’antiquité, on a découvert que régissait l’équilibre architectural du corps humain.
Le nombril divise le corps suivant le nombre d’or. Il doit correspondre au rapport entre taille totale et la hauteur du sol au nombril . C’est encore qui doit régler le rapport harmonieux entre la hauteur et la largeur d’une tête humaine. Ce dernier exemple, nous amène au canon de proportion de Vitruve, dessiné par Léonard de Vinci, datant du XV siècle, souvent utilisé.
Les rapports corporels qui sont conformes avec le nombre d’or : hauteurcorps humain / hauteurnombril :
-La distance entre la ligne de l’épaule et le sommet de la tête / la longueur de la tête
-La distance du nombril au sommet de la tête / la distance de la ligne de l’épaule au sommet de la tête
-La distance du nombril au genou / la distance du genou à la plante des pieds.
-La distance entre les extrémités des doigts et le coude / la distance entre le poignet et le coude

Nous avons également chacun sur 1 main : 5 doigts , chacun composé de 3 parties , séparées par 2 jointures. 5,3,2,1…
Application
Au moyen âge, les bâtisseurs de cathédrales utilisaient une tige constituée de cinq tiges articulées, correspondant chacune à une unité de mesure de l’époque, relatives au corps humain : la paume, la palme, l’empan, le pied et la coudée.
Les longueurs étaient données en lignes, une ligne mesurant environ 2 mm (précisément 2,247 mm) : Les partages du QUINE forment une suite additive, chaque dimension est la somme des deux précédentes, comme dans la suite de Fibonacci :
COUDE = PIED + EMPAN
PIED = EMPAN + PALME
EMPAN = PALME + PAUME
Selon les pays, les époques, les régimes, les religions ou les monuments les mesures de bases étaient différentes mais la progression était semblable.
Relation rectangle d’or / spirale / oreille.
On retrouve une application directe de cette spirale au niveau de l’oreille, une spirale qui est inscrite dans un rectangle d’or.
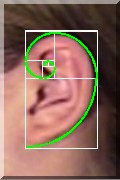
Mais le plus spectaculaire est la spirale dans notre glande pinéale.
Glande pinéale
La glande pinéale ou épiphyse est une petite glande endocrine de l’épithalamus du cerveau des vertébrés. À partir de la sérotonine, elle sécrète la mélatonine et joue donc, par l’intermédiaire de cette hormone, un rôle central dans la régulation des rythmes biologiques (veille/sommeil et saisonniers). Elle est également également comme notre 3 ème œil.
Cette glande a la forme d’une pomme de pin, d’où son nom et toute la symbolique qui en découle depuis les premières civilisations.
Mais ceci est une autre histoire…
Conclusion
Le nombre d’or est très présent dans la nature, et de multiples façons différente (galaxie, ouragan, etc) mais la raison de son apparition aussi bien chez les végétaux que chez les animaux et les hommes, reste un mystère.
On observe cependant, que le nombre d’or permet un arrangement optimal permettant une efficacité maximum (pour les feuilles sur une tige vis à vis de la lumière par exemple).
De plus, l’apparition du nombre d’or semble aussi lié en grande partie à des phénomènes de physique, de dynamique, qui s’appliquent dès le début de la formation de l’être vivant animal ou végétal. Il ne semble pas y avoir de prédispositions génétiques, comme on l’a longtemps pensé.
Le nombre d’or a également fasciné les première civilisations, et s’est rependu de manière spectaculaire dans les arts et l’ésotérisme. D’où le commencement de notre cheminement.
Vous aimerez aussi

L’ésotérisme du nombre d’or

Ankh

Le nœud-Tyet, le sang menstruel d’Isis

Le symbolisme du scarabée
Mon Instagram
Un ancêtre est un défunt qui a eu les rites funéraires nécessaires pour accéder à l`ancestralité. Il est comme une étoile autonome qui va agir en retour pour le bien et la prospérité de sa descendance. Mais si ses yich ka foutè fè, rien ne l`oblige à agir. Surtout si sa descendance ne le capte même plus.
De ce fait, il va boire son petit thé d`atoumo et manger ses pop-corn en regardant la télénovela de notre vie. Tôt ou tard, an piti ké vini rélé`y...donc il patiente.
N`oubliez pas un ancêtre est autonome, i pa bizwen`w ankò pou fè zafè`y. Mais par compassion suite à la rupture de la transmission familiale pendant de nombreux siècles, i toujou ka fè dé twa bagay an soumsoum pou ba`w fòs-la. Dèlè zot ka di sé bondié...zansèt ka toufé mé yo ka fè`y.
Mais attention lorsque la conjecture est favorable pour la reconnaissance qu`ils méritent et qu`ils ne l`ont pas pour x raisons, alors là lè zot ké pliché yo pé ké vini rilévè`w ankò.
Rélé bondié pou wè.
#fokousav
Je suis heureuse de vous annoncer la sortie prochaine (01 octobre) de mon deuxième roman Sen déyè Djab aux éditions @jets_dencre 🥳.
Dans un délire humoristique, philosophique, sarcastique et initiatique j`ai voulu retranscrire la bible Martiniquaise.
Et oui la bible en soumsoum qui se conte sans jamais se révéler au grand jour à travers les évangiles de Soraya et de Man Joliba. En effet, la femme a toute sa place dans notre histoire rocambolesque.
Disponible en librairie.
#livres #littérature #caraïbe #livrespeyi #booklover
#book #litteraturecaribeenne
Oui oui, c’est bien cela, vous avez bien lu ! Après 3 histoires insensées, il est temps de prendre un autre cap. Celui de l’Amour et non de la perdition. Que nos esprits corrompus par le vice puissent retrouver un peu de sensibilité au romantisme. C’est à cause de notre comportement impie que le zouk a disparu (é man paré ba kankan-an s`il le faut) car l’Amour est devenu une blague.
Et je n`aime pas le sucre dans mon thé. Merci
#séviskini






Laissez un commentaire